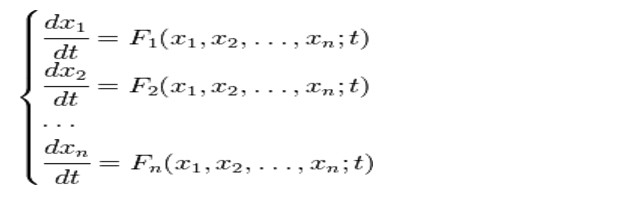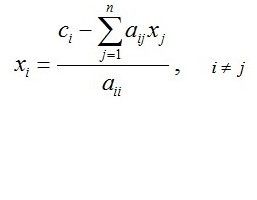Приклади систем лінійних рівнянь: метод рішення

Системи рівнянь отримали широке застосування векономічної галузі при математичному моделюванні різних процесів. Наприклад, при вирішенні завдань управління і планування виробництва, логістичних маршрутів (транспортна задача) або розміщення устаткування.

Системи рівняння використовуються не тільки в області математики, а й фізики, хімії та біології, при вирішенні задач по знаходженню чисельності популяції.

Системою лінійних рівнянь називають два і більшерівняння з багатьма змінними, для яких необхідно знайти спільне рішення. Таку послідовність чисел, при яких всі рівняння стануть вірними равенствами або довести, що послідовності не існує.

лінійне рівняння

Рівняння виду ax + by = c називають лінійними. Позначення x, y - це невідомі, значення яких треба знайти, b, a - коефіцієнти при змінних, c - вільний член рівняння.
Рішення рівняння шляхом побудова його графіка матиме вигляд прямої, всі крапки якої є рішенням многочлена.

Види систем лінійних рівнянь

Найбільш простими вважаються приклади систем лінійних рівнянь з двома змінними X і Y.

F1 (x, y) = 0 і F2 (x, y) = 0, де F1,2 - функції, а (x, y) - змінні функцій.

Вирішити систему рівнянь - це означає знайти такі значення (x, y), при яких система перетворюється в правильну рівність або встановити, що підходять значень x і y не існує.

Пара значень (x, y), записана у вигляді координат точки, називається рішенням системи лінійних рівнянь.

Якщо системи мають одне спільне рішення або рішення не існує їх називають рівносильними.

Однорідними системами лінійних рівнянь є системи права частина яких дорівнює нулю. Якщо права після знака "рівність" частина має значення чи виражена функцією, така система неоднорідна.

Кількість змінних може бути набагато більше двох, тоді слід говорити про приклад системи лінійних рівнянь з трьома змінними або більше.

Стикаючись з системами школярі припускають,що кількість рівнянь обов'язково має збігатися з кількістю невідомих, але це не так. Кількість рівнянь в системі не залежить від змінних, їх може бути як завгодно багато.

Прості і складні методи вирішення систем рівнянь

Не існує загального аналітичного способувирішення подібних систем, всі методи засновані на численних рішеннях. У шкільному курсі математики докладно описані такі методи як перестановка, алгебраїчне додавання, підстановка, а так же графічний і матричний спосіб, рішення методом Гаусса.

Основне завдання при навчанні способам вирішення -це навчити правильно аналізувати систему і знаходити оптимальний алгоритм рішення для кожного прикладу. Головне не визубрити систему правил і дій для кожного способу, а зрозуміти принципи застосування того чи іншого методу

Рішення прикладів систем лінійних рівнянь 7класу програми загальноосвітньої школи досить просте і пояснено дуже докладно. У будь-якому підручнику математики цього розділу відводиться досить уваги. Рішення прикладів систем лінійних рівнянь методом Гаусса і Крамера більш детально вивчають на перших курсах вищих навчальних закладів.

Рішення систем методом підстановки

Дії методу підстановки спрямовані навираз значення однієї змінної через другу. Вираз підставляється в час, що залишився рівняння, потім його приводять до вигляду з однією змінною. Дія повторюється в залежності від кількості невідомих в системі

Наведемо рішення прикладу системи лінійних рівнянь 7 класу методом підстановки:

Як видно з прикладу, змінна x була вираженачерез F (X) = 7 + Y. Отриманий вираз, підставлену під 2-е рівняння системи на місце X, допомогло отримати одну змінну Y у 2-е рівнянні. Рішення даного прикладу не викликає труднощів і дозволяє отримати значення Y. Останній крок це перевірка отриманих значень.

Вирішити приклад системи лінійних рівняньпідстановкою не завжди можливо. Рівняння можуть бути складними і вираз змінної через другу невідому виявиться занадто громіздким для подальших обчислень. Коли невідомих в системі більше 3-х рішення підстановкою також недоцільно.

Рішення прикладу системи лінійних неоднорідних рівнянь:

Рішення за допомогою алгебраїчного додавання

При пошуку рішення систем методом складання виробляють почленное додавання і множення рівнянь на різні числа. Кінцевою метою математичних дій є рівняння з однією змінною.

Для застосувань даного методу необхідна практикаі спостережливість. Вирішити систему лінійних рівнянь методом складання при кількості змінних 3 і більше непросто. Алгебраїчне додавання зручно застосовувати коли в рівняннях присутні дробу і десяткові числа.

Алгоритм дій рішення:

1. Помножити обидві частини рівняння на деяке число. В результаті арифметичної дії один з коефіцієнтів при змінній повинен стати рівним 1.
2. Почленно скласти отриманий вираз і знайти одне з невідомих.
3. Підставити отримане значення в 2-е рівняння системи для пошуку залишилася змінної.

Спосіб вирішення введенням нової змінної

Нову змінну можна вводити, якщо в системі потрібно знайти рішення не більше ніж для двох рівнянь, кількість невідомих теж має бути не більше двох.

Спосіб використовується, щоб спростити одне зрівнянь, введенням нової змінної. Нове рівняння вирішується щодо введеної невідомої, а отримане значення використовується для визначення початкової змінної.

З прикладу видно, що ввівши нову змінну t вдалося звести 1-е рівняння системи до стандартного квадратному тричленну. Вирішити многочлен можна відшукавши дискриминант.

Необхідно знайти значення дискримінанту повідомою формулою: D = b2 - 4 * a * c, де D - шуканий дискриминант, b, a, c - множники многочлена. У заданому прикладі a = 1, b = 16, c = 39, отже, D = 100. Якщо дискримінант більше нуля, то рішень два: t = -b ± √D / 2 * a, якщо дискримінант менше нуля, то рішення одне: x = -b / 2 * a.

Рішення для отриманих в результаті системи знаходять методом складання.

Наочний метод вирішення систем

Підходить для систем з 3-ма рівняннями. Метод полягає в побудові на координатної осі графіків кожного рівняння, що входить в систему. Координати точок перетину кривих і будуть спільним рішенням системи.

Графічний спосіб має ряд нюансів. Розглянемо кілька прикладів вирішення систем лінійних рівнянь наочним способом.

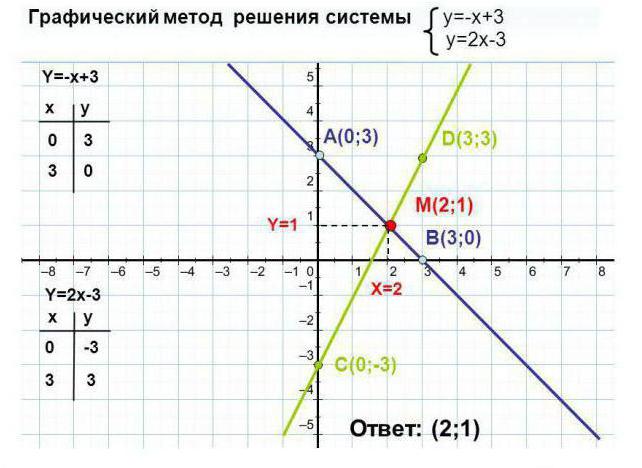
Як видно з прикладу, для кожної прямої булопобудовано дві точки, значення змінної x були обрані довільно: 0 і 3. Виходячи зі значень x, знайдені значення для y: 3 і 0. Точки з координатами (0, 3) і (3, 0) були відзначені на графіку і з'єднані лінією .

Дії необхідно повторити для другого рівняння. Точка перетину прямих є розв'язком системи.

У наступному прикладі потрібно знайти графічне рішення системи лінійних рівнянь: 0,5x-y + 2 = 0 і 0,5x-y-1 = 0.

Як видно з прикладу, система не має рішення, тому що графіки паралельні і не перетинаються на всьому своєму протязі.

Системи із прикладів 2 і 3 схожі, але припобудові стає очевидно, що їх рішення різні. Слід пам'ятати, що не завжди можна сказати чи має система рішення чи ні, завжди необхідно побудувати графік.

Матриця і її різновиди

Матриці використовуються для короткої записи системи лінійних рівнянь. Матрицею називають таблицю спеціального виду, заповнену числами. Матриця виду n * m має n - рядків і m - стовпців.

Матриця є квадратної, коли кількістьстовпців і рядків одно між собою. Матрицею - вектором називається матриця з одного стовпця з нескінченно можливою кількістю рядків. Матриця з одиницями по одній з діагоналей і іншими нульовими елементами називається одиничною.

Зворотній матриця - це така матриця при множенні на яку вихідна перетворюється в одиничну, така матриця існує тільки для вихідної квадратної.

Правила перетворення системи рівнянь в матрицю

Стосовно до систем рівнянь в якості чисел матриці записують коефіцієнти і вільні члени рівнянь, одне рівняння - один рядок матриці.

Рядок матриці називається ненульовий, якщо хоча бодин елемент рядки не дорівнює нулю. Тому якщо в якомусь із рівнянь кількість змінних різниться, то необхідно на місці відсутньої невідомої вписати нуль.

Стовпці матриці повинні строго відповідатизмінним. Це означає що коефіцієнти змінної x можуть бути записані тільки в один стовпець, наприклад перший, коефіцієнт невідомої y - тільки в другій.

При множенні матриці всі елементи матриці послідовно множаться на число.

Варіанти знаходження оберненої матриці

Формула знаходження оберненої матриці досить проста: K^-1= 1 / | K |, де K^-1 - зворотна матриця, а | K | - визначник матриці. | K | не повинен бути рівний нулю, тоді система має рішення.

Визначник легко обчислюється для матриці "два на два", необхідно лише помножити один на одного елементи по діагоналі. Для варіанту "три на три" існує формула | K | = a₁b₂c₃ + a₁b₃c₂ + a₃b₁c_{2 +} a₂b₃c₁ + a₂b₁c₃ + a₃b₂c₁. Можна скористатися формулою, а можназапам'ятати що необхідно взяти по одному елементу з кожного рядка і кожного стовпця так, щоб в творі не повторювалися номери стовпців і рядків елементів.

Рішення прикладів систем лінійних рівнянь матричним методом

Матричний спосіб пошуку рішення дозволяє скоротити громіздкі записи при вирішенні систем з великою кількістю змінних і рівнянь.

У прикладі a_nm - коефіцієнти рівнянь, матриця - вектор x_n - змінні, а b_n - вільні члени.

Далі необхідно знайти зворотну матрицю і помножити на неї вихідну. Знайти значення змінних в отриманої одиничної матриці легко здійсненне завдання.

Рішення систем методом Гаусса

У вищій математиці спосіб Гаусса вивчаютьспільно з методом Крамера, а процес пошуку рішення систем так і називається метод вирішення Гаусса - Крамера. Дані способи використовують при знаходженні змінних систем з великою кількістю лінійних рівнянь.

Метод Гаусса дуже схожий на рішення за допомогоюпідстановок і алгебраїчного додавання, але більш систематичний. У шкільному курсі рішення способом Гаусса застосовується для систем з 3 і 4 рівнянь. Мета методу полягає в приведенні системи до виду перевернутої трапеції. Шляхом алгебраїчних перетворень і підстановок знаходиться значення однієї змінної в одному з рівнянні системи. Друге рівняння являє собою вираз з 2-ма невідомими, ну а 3 і 4 - відповідно з 3-ма та 4-ма змінними.

Після приведення системи до описаного виду, подальше рішення зводиться до послідовної підстановці відомих змінних в рівняння системи.

У шкільних підручниках для 7 класу приклад рішення методом Гаусса описаний таким чином:

Як видно з прикладу, на кроці (3) було отримано два рівняння 3x₃-2x₄= 11 і 3x₃+ 2x₄= 7. Рішення будь-якого з рівнянь дозволить дізнатися одну з змінних x_n.

Теорема 5, про яку згадується в тексті, говорить що якщо одне з рівнянь системи замінити рівносильним, то отримана система буде також рівносильна вихідної.

Метод Гаусса важкий для сприйняття учнівсередньої школи, але є одним з найбільш цікавих способів для розвитку кмітливості дітей, які навчаються за програмою поглибленого вивчення в математичних і фізичних класах.

Для простоти запису обчислень прийнято робити в такий спосіб:

Коефіцієнти рівнянь і вільні членизаписуються у вигляді матриці, де кожен рядок матриці співвідноситься з одним з рівнянь системи. Вертикальна риса відокремлює ліву частину рівняння від правої. Римськими цифрами позначаються номера рівнянь в системі.

Спочатку записують матрицю, з якою доведетьсяпрацювати, потім всі дії проводяться з однією з рядків. Отриману матрицю записують після знака "стрілка" і продовжують виконувати необхідні алгебраїчні дії до досягнення результату.

У результаті повинна вийти матриця в якій пооднією з діагоналей стоять 1, а всі інші коефіцієнти рівні нулю, тобто матрицю призводять до одиничного виду. Не можна забувати робити обчислення з цифрами обох частин рівняння.

Даний спосіб записи менш громіздкий і дозволяє не відволікатися на перерахування численних невідомих.

Вільне застосування будь-якого способу вирішеннязажадає уважності і певного досвіду. Не всі методи мають прикладний характер. Якісь способи пошуку рішень є кращими в тій чи іншій області діяльності людей, а інші існують в цілях навчання.